Probability
of Inheritance
The value of
studying genetics is in understanding how we can
predict the likelihood of inheriting particular traits. This can help plant and
animal breeders in developing varieties that have more desirable qualities. It can
also help people explain and predict patterns of inheritance in family lines.
One of the
easiest ways to calculate the mathematical probability of inheriting a specific trait was
invented by an early 20th century English geneticist named Reginald Punnett
 . His
technique employs what we now call a Punnett square.
This is a simple graphical way of discovering all of the potential combinations of
genotypes that can occur in children, given the
genotypes of their parents. It also shows us the odds of each of the offspring
genotypes occurring.
. His
technique employs what we now call a Punnett square.
This is a simple graphical way of discovering all of the potential combinations of
genotypes that can occur in children, given the
genotypes of their parents. It also shows us the odds of each of the offspring
genotypes occurring.
Setting up
and using a Punnett square is quite simple once you understand how it works.
You begin by drawing a grid of perpendicular lines:
Next, you put
the genotype of one parent across the top and that of the other parent down the left
side. For example, if parent pea plant genotypes were YY and GG respectively, the
setup would be:
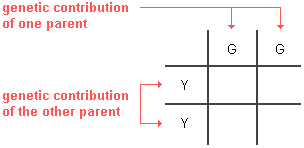
Note that
only one letter goes in each box for the parents. It does not matter which parent
is on the side or the top of the Punnett square.
Next,
all you have to do is fill in the boxes by copying the row and column-head
letters across or down into the empty squares. This gives us the
predicted frequency of all of the potential genotypes among the offspring each
time reproduction occurs.
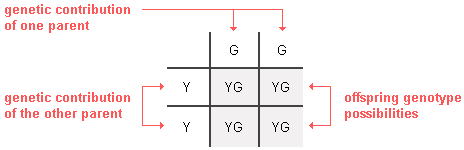
In this
example,
100% of the offspring will likely be heterozygous
(YG). Since the Y (yellow) allele is dominant over the G (green) allele for pea
plants, 100% of the YG offspring will have a yellow phenotype,
as Mendel observed in his breeding experiments.
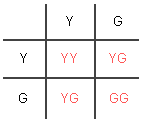
In another
example (shown below), if the parent plants both have heterozygous (YG) genotypes, there
will be 25% YY, 50% YG, and 25%
GG offspring on average. These percentages are
determined based on the fact that each of the 4 offspring boxes in a Punnett square is 25%
(1 out of 4). As to phenotypes, 75% will be Y and only 25% will be
G. These
will be the odds every time a new offspring is conceived by parents with YG
genotypes.
An offspring's genotype is the result of the combination of genes in the sex
cells or gametes (sperm and ova) that came together in its conception.
One sex cell came from each parent. Sex cells normally only have one
copy of the gene for each trait (e.g., one copy of the Y or G form of the gene
in the example above). Each of the two Punnett square boxes in which the
parent genes for a trait are placed (across the top or on the left side)
actually represents one of the two possible genotypes for a parent sex
cell. Which of the two parental copies of a gene is inherited depends on
which sex cell is inherited--it is a matter of chance. By placing each
of the two copies in its own box has the effect of giving it a 50% chance of
being inherited.
If you are
not yet clear about how to make a Punnett Square and interpret its result, take the time to try to figure it out before going on.
Are Punnett Squares Just Academic
Games?
Why is it important for you to know
about Punnett squares? The answer is that they can be used as predictive
tools when considering having children. Let us assume, for instance, that
both you and your mate are carriers for a particularly
unpleasant genetically inherited disease such as
cystic fibrosis
 . Of course, you are worried about whether your children will be healthy
and normal. For this example, let us define "A" as being
the dominant normal allele and "a" as the recessive
abnormal one that is responsible for cystic fibrosis. As carriers, you and your
mate are both heterozygous (Aa). This disease only
afflicts those who are homozygous recessive (aa).
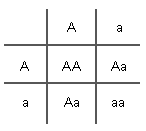
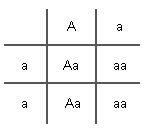
The Punnett square below makes it clear that at each birth, there will be a 25% chance of
you having a normal homozygous (AA) child, a 50% chance of a healthy
heterozygous (Aa) carrier child like you and your mate, and a
25% chance of a homozygous recessive (aa) child who probably
will eventually die from this condition.
. Of course, you are worried about whether your children will be healthy
and normal. For this example, let us define "A" as being
the dominant normal allele and "a" as the recessive
abnormal one that is responsible for cystic fibrosis. As carriers, you and your
mate are both heterozygous (Aa). This disease only
afflicts those who are homozygous recessive (aa).
The Punnett square below makes it clear that at each birth, there will be a 25% chance of
you having a normal homozygous (AA) child, a 50% chance of a healthy
heterozygous (Aa) carrier child like you and your mate, and a
25% chance of a homozygous recessive (aa) child who probably
will eventually die from this condition.
 |
|
 |
|
If both parents are carriers of the
recessive
allele for a disorder, all of their children will
face
the following odds of inheriting it:
25% chance of having the recessive disorder
50% chance of being a healthy carrier
25% chance of being healthy and not have
the recessive allele at all |
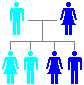
If
a carrier (Aa) for such a
recessive disease mates with someone who has it (aa), the likelihood of their children also inheriting the condition is far greater
(as shown below). On average, half of the children will be heterozygous (Aa) and, therefore, carriers. The
remaining half will inherit 2 recessive alleles (aa) and develop the disease.
 |
|
 |
|
If one parent is a carrier and the
other has a
recessive disorder, their children will have the
following odds of inheriting it:
50% chance of being a healthy carrier
50% chance having the recessive disorder |
It is likely that every one of us is a carrier
for a large number of recessive alleles. Some of these alleles can cause life-threatening defects if they are inherited from both
parents. In addition to cystic fibrosis, albinism, and
beta-thalassemia are recessive disorders.
Some disorders are caused by dominant alleles for genes.
Inheriting just one copy of such a dominant allele will cause the disorder.
This is the case with Huntington disease, achondroplastic dwarfism, and
polydactyly. People who are heterozygous (Aa) are not healthy carriers.
They have the disorder just like homozygous dominant (AA) individuals.
 |
|
 |
|
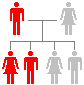
If only one parent has a single copy
of a
dominant allele for a dominant disorder,
their children will have a 50% chance of
inheriting the disorder and 50% chance
of being
entirely normal. |
Punnett squares are standard tools used by
genetic counselors. Theoretically,
the likelihood of inheriting many traits, including useful ones, can be predicted using
them. It is also possible to construct squares for more than one trait
at a time. However, some traits are not inherited with the
simple mathematical probability suggested here. We will explore some of these
exceptions in the next section of the tutorial.
Copyright © 1997-2012 by Dennis
O'Neil.
All rights reserved.
illustration credits
![]() . His
technique employs what we now call a Punnett square.
This is a simple graphical way of discovering all of the potential combinations of
genotypes that can occur in children, given the
genotypes of their parents. It also shows us the odds of each of the offspring
genotypes occurring.
. His
technique employs what we now call a Punnett square.
This is a simple graphical way of discovering all of the potential combinations of
genotypes that can occur in children, given the
genotypes of their parents. It also shows us the odds of each of the offspring
genotypes occurring.







